Condiciones de Contorno.

Una ida de la olla, tercera parte.

Prólogo.

En la entrada anterior (de esta serie) comenté de la complejidad de las fórmulas matemáticas que aplican a los servosistemas, así como de los límites.

De esto va esta entrada, de límites, y de expresiones matemáticas (que no veremos, no os asustéis), y de realidades físicas.

De cómo eso afecta a la dinámica de sistemas.

De cómo los sistemas realimentados funcionan sólo dentro de unos límites, de cómo cuando se salen de esos límites la cosa cambia, y de cuales pueden ser esos límites.

Y a esos límites, en matemáticas, así como en electrónica, se les conoce con una expresión que utilizo a menudo: las Condiciones de Contorno.

Aquellas cosas que afectan el contorno de funcionamiento correcto y fuera de las cuales, el comportamiento empieza a ser errático en el mejor de los casos, o contraproducente en la mayoría de ellos.

En la siguiente entrada de esta serie, por fin para los lectores, veremos dónde conduce todo este hilo de pensamiento y cómo estas condiciones de contorno son tan importantes para determinar lo que puede y no puede pasar en las épocas oscuras que tenemos por delante.

Un muelle, de nuevo.

El ejemplo de referencia de todo este entramado, por su simplicidad aparente, es el muelle, y como hemos dicho, el principio de funcionamiento básico es la Ley de Hooke:

F = -K·(X – X₀)

Esa es la misma fórmula matemática que puse en la anterior entrada, podría decir con matices, que “la única que veremos” (hay otra muy similar en la próxima entrada, razón de fondo de todo este jaleo).

Como dije, aquí no aparece ninguna función tipo Seno o Coseno de X, y sin embargo, sabemos que el resultado oscila siguiendo precisamente una función Seno (o Coseno, esto suele ir a gustos: ante la duda…).

Eso es debido a que la función que he puesto arriba no es la única que aplica al sistema. Si tenemos una masa suspendida, aparecen por un lado la gravedad como una (fuerza) constante que tira hacia abajo, las leyes de Newton que relacionan movimiento de una masa con las fuerzas que aplican sobre la misma (la del muelle y la de la gravedad), etc.

El resultado real es un sistema de ecuaciones diferenciales, habitualmente resueltas (en electrónica) mediante Laplace, y que suele dar, de forma invariante, una solución en base a una exponencial compleja (en el sentido matemático del término, pero que además es muy adecuado en el sentido literal).

Pero eso aplica sí y sólo sí la función aquí expuesta es única e invariante.

¿Qué quiere decir eso de invariante?

Que en toda la “zona” de aplicación, esa ley se cumple en su totalidad.

Pero resulta que en la realidad física en la que vivimos, esa “zona” de aplicación está limitada.

En el caso del muelle, si lo comprimimos demasiado, las espiras del mismo se tocan, y deja de funcionar como funcionaba antes debido a ese contacto: no se puede comprimir más (en realidad, sí, pero la K se dispara varios órdenes de magnitud, hay que hacer toneladas de fuerza) y, de hacerlo, se estropea el muelle.

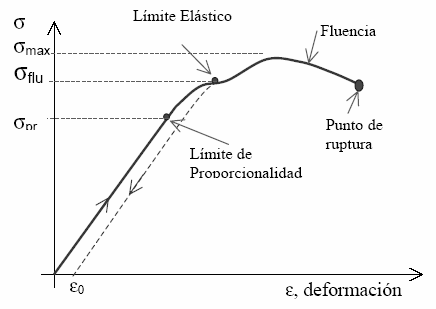
Si tiramos hacia el otro lado, el resultado es que, a partir de cierto estiramiento, de cierta elongación, el muelle no recupera su forma original, a partir de cierto punto, no recupera nada, y si seguimos tirando, no sólo cuesta menos el estirarlo, encima acaba rompiéndose.

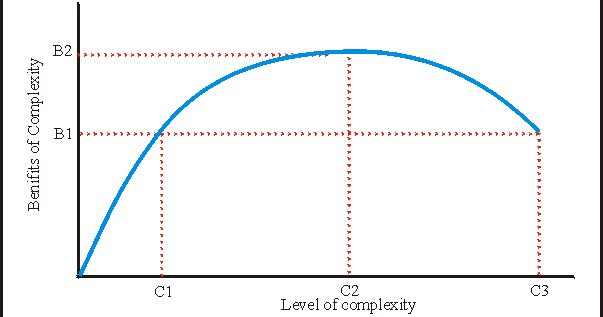
Si hacemos una gráfica de la fuerza aplicada al muelle contra la distancia que se contrae o alarga, nos sale una curva muy típica.

Una curva a la que llamo La Curva de Tainter, que, dicho sea de paso, viene de un estudio totalmente diferente.

En esa curva, vemos que por la izquierda, llega un momento en que no se puede comprimir más el muelle, un punto muy concreto y muy fácil de identificar, un “límite duro”. Una X mínima.

Por el otro lado, tenemos todo lo contrario: el punto en que la fuerza deja de seguir la fórmula propuesta no es nada fácil de determinar, y encima, no “molesta”.

Si se estira un poco más, además de necesitar menos fuerza de la calculada, llega un punto que al soltar el muelle, éste no recupera exactamente su posición original, pero continúa funcionando.

Sin embargo, el resultado ya es diferente puesto que el punto de equilibrio, funcional aún, ha cambiado.

Si aún estiramos más, continuamos teniendo un “déficit de fuerza”, ya más notable, pero con una deformación cada vez más grande, y habitualmente además con una K más débil: se ha sobrepasado el margen de elasticidad del muelle, y el funcionamiento cada vez es menos parecido al calculado, ya no sólo por una X₀ diferente, también ha cambiado la K.

Si seguimos estirando, llega un momento en que la fuerza para alargarlo incluso es menor que la que necesitábamos antes: es el pico de elasticidad.

A estas alturas, ya ni recupera la forma, ni la funcionalidad. El muelle ha quedado inservible.

Si seguimos estirando, llega el punto final, la ruptura del muelle, a una fuerza más baja que la del pico.

Este “límite por la derecha” es un límite difuso, un límite blando, relativo, de difícil determinación, y que una vez se ha sobrepasado, cambia totalmente la dinámica del sistema, la funcionalidad, el resultado, hasta llegar a funcionar al revés (la fuerza aplicada disminuye, no aumenta) de lo previsto.

Esa X máxima difícil de determinar marca el otro extremo de las Condiciones de Contorno.

Podemos decir que el sistema funciona siempre y cuando se apliquen ciertas Condiciones: que la X esté entre la X mínima y la X máxima.

Fuera de esta zona, delimitada por este contorno, el sistema deja de funcionar y lo que obtenemos no tiene por qué ser lo que deseamos.

Es el choque con los límites.

Un inciso.

Bajo determinadas condiciones de contorno, hemos visto, el resultado puede ser no sólo diferente, sino el contrario a lo previsto.

No es necesario salirse de estas condiciones de contorno para que el funcionamiento sea el contrario de lo previsto.

En muchos sistemas realimentados, es lo habitual que suceda, no es nada raro que un exceso de realimentación cambia el sentido de funcionamiento, haciendo que funcione justo al revés de lo previsto.

¿Recordamos el signo negativo, ese que implica realimentación negativa?

Un ejemplo muy curioso de sistema realimentado, inesperado para mucha gente, está en nuestra mente. Si, nuestro cuerpo está repleto de sistemas realimentados, y la próxima entrada explicará algunos de estos sistemas realimentados particulares, aunque hoy, ante la brevedad de esta entrada, aprovecho para adelantar un ejemplo que poca gente espera, que es ilustrativo, y que subraya el concepto secundario de esta entrada: la inversión del resultado.

¿Alguna vez ha escuchado, amable lector, la expresión Trastorno de Déficit de Atención e Hiperactividad, TDAH?

Entre los que somos padres, este es un elemento conocido, y es uno de los campos más trabajados (y malinterpretados) de la psicología.

Entre aquellas personas que padecen este trastorno, y que han sido correctamente diagnosticadas (eso es algo importante que analizaremos otro día), se les suelen dar “medicamentos maravillosos” que devuelven la “normalidad” a los pacientes (bueno, a veces se pasan hacia el otro extremo).

Lo curioso, es cuales son estos medicamentos maravillosos: excitantes como las anfetaminas.

Sí, sí. La “cura” para la hiperactividad es dar potenciadores de la actividad, excitantes.

Justo lo contrario a lo que la gente cree.

¿Por qué eso?

Pues porque la mente tiene muchos servosistemas dentro, una buena parte a nivel molecular (el caso del glutamato que veremos en la próxima entrada), pero, en este caso, a nivel de Sistema Complejo.

Resulta que por alguna razón, el cerebro no recibe suficiente “estímulo” de entrada, así que el sistema de compensación está todo el rato buscando ese estímulo externo. Al no llegar en la cantidad necesaria, cambia de tema (déficit de atención: lo que le ha llamado la atención no cubre la necesidad del cerebro de estímulo, así que lo deja de lado y va a otro), o se lanza a hacer cosas frenéticamente (aumenta el ritmo para ver si así consigue el nivel deseado de estímulo).

Obviamente el tema es mucho más complejo, complicado, largo de explicar, repleto de conceptos neuronales, psicológicos, biológicos, etc.

Pero la forma de entenderlo básica, simplificada, el formato más abstracto, es precisamente este: la Dinámica del Sistema de Gestión de Estímulos del cerebro, un sistema realimentado, está “mal sintonizado” (el problema puede deberse a muchos factores, como ya he comentado, debido a la complejidad).

Así pues, la Dinámica de Sistemas en muchas ocasiones funciona al revés de lo previsto debido precisamente a esa realimentación.

Otro ejemplo, a nivel social, sería el Principio de Shirky.

Ida de la Olla nº3.

Por tanto, en esta entrada de hoy nos encontramos con dos conceptos relacionados, dos principios básicos de todos los sistemas realimentados

El primero, que estos sistemas funcionan correctamente, según lo previsto, dentro de una zona, área, delimitada por lo que llamaremos Condiciones de Contorno. Fuera de estos límites, que pueden ser complejos de determinar, incluso al acercarnos a dichos límites, el funcionamiento no sólo cambia, puede estropearse, dejar de funcionar, colapsar el sistema al completo, etc.

El segundo concepto, es que incluso dentro de las Condiciones de Contorno, un servosistema puede funcionar al revés de lo intuitivamente previsto. Cuando nos acercamos a los límites, especialmente si son límites blandos, difusos, poco evidentes, mayor es la probabilidad de ese funcionamiento inverso.

La próxima entrada será mucho más interesante: veremos cómo toda esta ida de la olla aplica al mundo real, al mundo humano, a la sociedad.

Beamspot.